Off-Axis Axial field of a finite solenoid

Off-Axis

Axial Field of a Finite Solenoid

The magnetic field in the central region of a solenoid can be approximated as a simple polynomial involving Legendre polynomials. Montgomery and Terrell state that "out to within a few percent of the inner radius of the coil, the field can be found quite accurately with only a few ... terms."

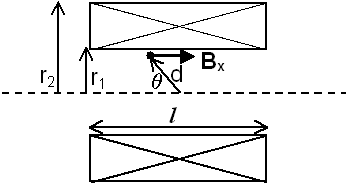
Solenoid in cross section view.

This polynomial can be written as:

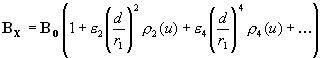
where,

B_O is the central field strength of the solenoid,

and the first four even numbered error coefficients, e _n, are:

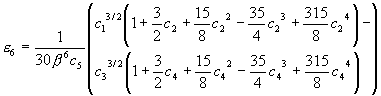
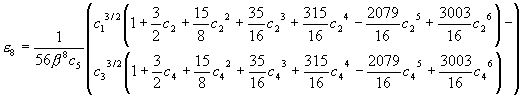
where:

, , , ,

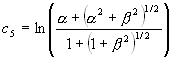
r₁, r₂, and l are inner, and outer coil radii, and coil length, respectively.

d is the distance from the coil center to the field measurement point,

q is the angle between the measurement point position vector and the coil axis,

and the corresponding Legendre polynomials, r_n, are:

where:

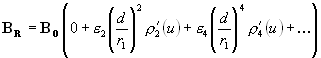
But What About Off-Axis Radial Field Components?

According to this reference, there is a corresponding series for obtaining the radial component of the magnetic field in the central region of a solenoid, which looks like this:

Where r ^l_n are derivatives of the even Legendre polynomials, such as:

where

It looks wonderful, except for the fact that the computed radial fields are wrong. I don't know why they're wrong, since the math is a little over my head. If you know the answer, please drop me a line.

Credits

The formulas on this page are adapted from:

SOME USEFUL INFORMATION FOR THE DESIGN OF AIR-CORE SOLENOIDS by D.Bruce Montgomery and J. Terrell., published November, 1961, under Air Force Contract AF19(604)-7344.

Montgomery and Terrell, in turn, credit:

M.W. Garrett, J. Appl. Phys. 22, 9, Sept. 1951.

I am developing an updated and expanded version of the magnet web site and encourage you to visit this work in progress and comment on what you see. As a self-employed software engineer trying to balance time between work and magnets, your encouragement in building this site is always welcome!

Please consider clicking the PayPal link and making a contribution to support the maintenance and development of this site. Thank you for visiting!

Magnet Formulas HOME | E-mail