Axial field of a finite solenoid

This formula uses the formula for the field due to a thin shell solenoid, integrated over a range off radii to obtain the magnetic field at any point on the axis of a finite solenoid.

Solenoid in cross section view.
General Case:  
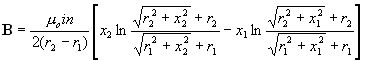  B is the magnetic field, in teslas, at any point on the axis of the solenoid. The direction of the field is parallel to the solenoid axis.

is the permeability constant (1.26x10-6 Tm/A, 1.26x10-4 Tcm/A or 4.95x10-5 Tin/A, for coils measured in meters, centimeters and inches, respectively)

i is the current in the wire, in amperes.

n is the number of turns of wire per unit length in the solenoid.

r1 is the inside radius of the solenoid.

r2 is the outside radius of the solenoid.

x1 and x2 are the distances, on axis, from the ends of the solenoid to the magnetic field measurement point.

Note that the units of length may be meters, centimeters or inches (or furlongs, for that matter), as long as the correct value of the permeability constant is used.
...or, for something really useful:

where G is the unitless geometry factor:

where , and

  P is the total power consumed by the coil, in watts.

is equal to (total conductor cross section area)/(total coil cross section area), which ranges from 0.6 to 0.8 in typical coils.

is the conductor resistivity, in units of ohms-length. The length units must match those of r1.
Special Case: x1=(-x2) The magnetic field measurement point is at the center of the solenoid.

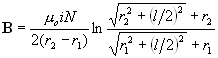...or
  j is the current density in the coil cross section, in amps/(unit area).

l is the length of the coil.

N is the total number of turns of wire in the coil.
and the unitless geometry factor G is simply:

 

  Note that G is maximum when and . A coil built with a given inner diameter and input power will deliver the highest central field strength when these conditions are met.

 

Magnet Formulas web site, © 2005 by Eric Dennison.

I am developing an updated and expanded version of the magnet web site and encourage you to visit this work in progress and comment on what you see. As a self-employed software engineer trying to balance time between work and magnets, your encouragement in building this site is always welcome!

Please consider clicking the PayPal link and making a contribution to support the maintenance and development of this site. Thank you for visiting!
click to visit emagnet v2 click to visit netdenizen.com studios

Magnet Formulas HOME | E-mail