On-Axis Field of a Finite Solenoid¶
This formula uses the formula for the field due to a thin shell solenoid, integrated over a range of radii to obtain the magnetic field at any point on the axis of a finite.
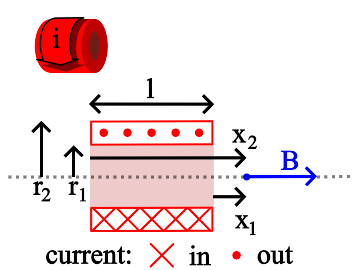
General Case¶
$B = \frac {\mu_o i n}{2 (r_2 - r_1)} \left [ x_2 \ln \left ( \frac {\sqrt{r_2^2 + x_2^2} + r_2}{\sqrt{r_1^2 + x_2^2} + r_1} \right ) - x_1 \ln \left ( \frac {\sqrt{r_2^2 + x_1^2} + r_2}{\sqrt{r_1^2 + x_1^2} + r_1} \right ) \right ]$
B is the magnetic field, in teslas, at any point on the axis of the solenoid. The direction of the field is parallel to the solenoid axis.
$\mathbf \mu_o$ is the permeability constant (1.26x10-6 Hm-1)
i is the current in the wire, in amperes.
n is the number of turns of wire per unit length in the solenoid.
r1 is the inner radius of the solenoid, in meters.
r1 is the inner radius of the solenoid, in meters.
r2 is the outer radius of the solenoid, in meters.
x1 and x2 are the distances, on axis, from the ends of the solenoid to the magnetic field measurement point, in meters.
The "G Factor"¶
The field can be expressed in a form that separates the unit system, power and winding configuration from the unitless geometry of the coil. This introduces the "G Factor":
$B = \mu_o G \sqrt \frac {P \lambda} {r_1 \rho}$
where G is the unitless geometry factor defined as:
$G = \sqrt{\frac {1}{8 \pi \beta (\alpha^2 - 1)}} \left [ (\gamma + \beta) \ln \left ( \frac {\alpha + \sqrt{\alpha^2 + (\gamma + \beta)^2}}{1 + \sqrt{1 + (\gamma + \beta)^2}} \right ) - (\gamma - \beta) \ln \left ( \frac {\alpha + \sqrt{\alpha^2 + (\gamma - \beta)^2}}{1 + \sqrt{1 + (\gamma - \beta)^2}} \right ) \right ]$
where,
$\alpha = \frac {r_2}{r_1}$, $\beta = \frac l {2 r_1}$ and $\gamma = \frac {x_1 + x_2}{2 r_1}$
P is the total power consumed by the coil, in watts.
$\lambda$ is equal to the total conductor cross section area divided by the total coil cross section area, which ranges from 0.6 to 0.8 in typical coils.
$\rho$ is the conductor resistivity, in units of ohms-length. The length units must match those of r1.
Special Case: x1 = -x2¶
When the magnetic field measurement point is at the center of the solenoid:
$B = \frac {\mu_o i N}{2(r_2 - r_1)} \ln \left ( \frac {\sqrt{r_2^2 + (\frac l 2)^2} + r_2}{\sqrt{r_1^2 + (\frac l 2)^2} + r_1} \right )$
or...
$B = \frac {\mu_o j l}{2} \ln \left ( \frac {\sqrt{r_2^2 + (\frac l 2)^2} + r_2}{\sqrt{r_1^2 + (\frac l 2)^2} + r_1} \right )$
j is the bulk current density in the coil cross section, in amperes per square meter.
l is the length of the solenoid, in meters.
N is the total number of turns of wire in the coil.
The unitless geometry factor G is simply:
$G = \sqrt \frac {\beta} {2 \pi (\alpha^2 - 1)} \ln \left ( \frac {\alpha + \sqrt{\alpha^2 + \beta^2}} {1 + \sqrt{1 + \beta^2}} \right )$
Note that G is maximum when $\alpha=3$ and $\beta=2$. A coil built with a given inner diameter and input power will deliver the highest central field strength when these conditions are met.
Code Example¶
The following Python code shows how to use these formulas to calculate magnetic fields.
%matplotlib inline
from scipy.special import ellipk, ellipe, ellipkm1
from numpy import pi, sqrt, linspace, log
from pylab import plot, xlabel, ylabel, suptitle, legend, show
uo = 4E-7*pi # Permeability constant - units of H/m
# Compute G Factor from unitless parameters
def GFactorUnitless(a, b, g=0.0): # alpha, beta - omit gamma for central
gpb2 = (g+b)*(g+b)
gmb2 = (g-b)*(g-b)
if not g == 0.0:
sq = sqrt(1/(8*pi*b*(a*a-1)))
t1 = (g+b)*log((a+sqrt(a*a+gpb2))/(1+sqrt(1+gpb2)))
t2 = (g-b)*log((a+sqrt(a*a+gmb2))/(1+sqrt(1+gmb2)))
B = sq*(t1-t2)
else:
sq = sqrt(b/2/pi/(a*a-1))
B = sq*log((a+sqrt(a*a+b*b))/(1+sqrt(1+b*b)))
return B
# Compute G Factor from all dimensions
def GFactor(r1, r2, l, x1=0.0, x2=0.0): # omit x1, x2 to compute central field
a = r2/r1
b = l/2/r1
g = (x1+x2)/2/r1
return GFactorUnitless(a, b, g)
# Compute B field on axis from unitless dimensions
def BFieldUnitless(power, packing, resistivity, r1, a, b, g=0.0):
return uo*GFactorUnitless(a, b, g)*sqrt(power*packing/r1/resistivity)
# Compute B field on axis from actual dimensions (x is measurement point - center if none)
def BField(power, packing, resistivity, r1, r2, length, x=0.0):
a = r2/r1
b = length/2/r1
g = x/r1
return BFieldUnitless(power, packing, resistivity, r1, a, b, g)
Now let's apply the B function to a typical coil. We'll assume copper (at resistivity of 1.68x10-8 ohm-m) conductors at a packing density of 0.75, inner radius of 1.25 cm, power of 100 W and with supposedly optimal $\alpha$ and $\beta$ of 3 and 2, respectively:
resistivity = 1.68E-8 # ohm-meter
r1 = 0.0125 # meter
packing = 0.75
power = 100.0 # watts
B = BFieldUnitless(power, packing, resistivity, r1, 3, 2)
print("B Field: {:.3} T".format(B))
Now try any combination of factors (assuming packing of 0.75 and standard copper conductors) to compute the field:
from ipywidgets import interactive
from IPython.display import display
def B(power, r1, r2, length, x):
return "{:.3} T".format(BField(power, 0.75, resistivity, r1, r2, length, x))
v = interactive(B,
power=(0.0, 200.0, 1),
r1 = (0.01, 0.1, 0.001),
r2 = (0.02, 0.5, 0.001),
length = (0.01, 2, 0.01),
x = (0.0, 4, 0.01))
display(v)
For a given inner radius, power and winding configuration, the field strength is directly proportional to G. Therefore, we can test the assertion that G is maximum when $\alpha$ is 3 and $\beta$ is 2 by constructing a map of G as a function of $\alpha$ and $\beta$:
from pylab import pcolor, colorbar, meshgrid, contour
from numpy import arange
a = arange(1.1, 6.0, 0.1)
b = arange(0.1, 4.0, 0.1)
A, B = meshgrid(a,b)
G = GFactorUnitless(A, B)
contour(A, B, G, 30)
colorbar()
xlabel("Unitless parameter, Alpha")
ylabel("Unitless parameter, Beta")
suptitle("Electromagnet 'G Factor'")
show()
print("G Factor at A=3, B=2: {:.3}".format(GFactorUnitless(3,2)))
print("G Factor at A=3, B=1.9: {:.3}".format(GFactorUnitless(3,1.9)))
Although it is apparent that the maximum G Factor occurs near the $\alpha=3$, $\beta=2$ point, it is not exactly so:
from scipy.optimize import minimize
def GMin(AB):
return -GFactorUnitless(AB[0], AB[1])
res = minimize(GMin, [3, 2])
print("G Factor is maximum at Alpha = {:.4}, Beta = {:.4}".format(*res.x))
Magnet Formulas, © 2018 by Eric Dennison. Source code and License on Github